Post-processing: realizzare mappe di velocità a iso-profondità

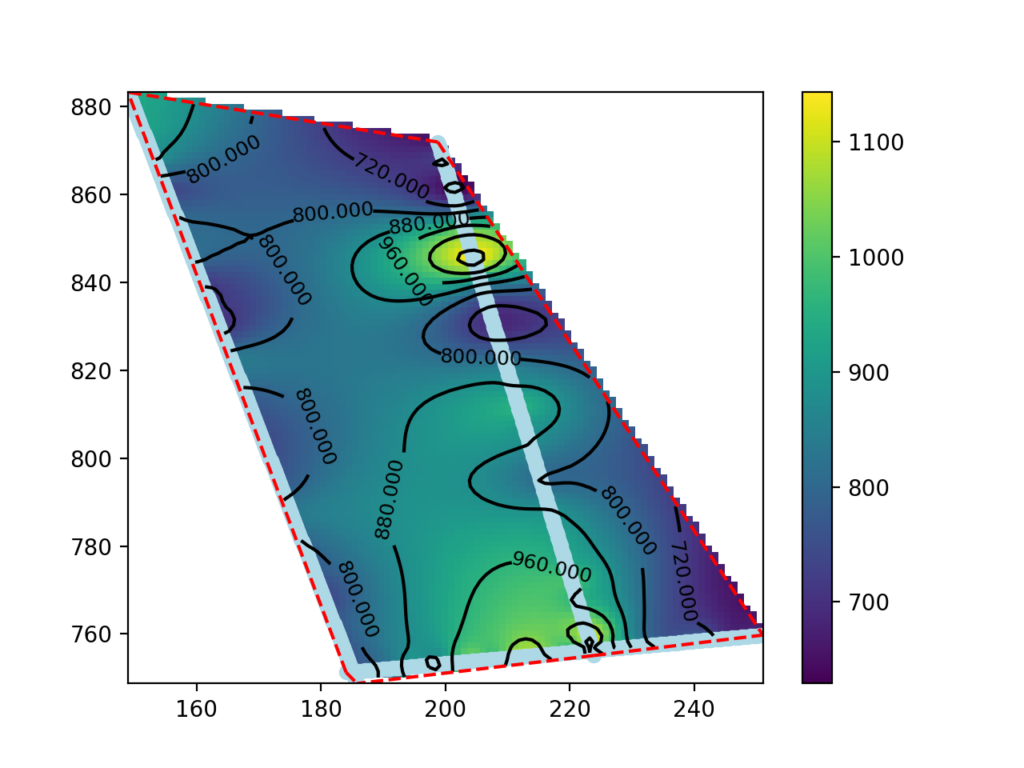
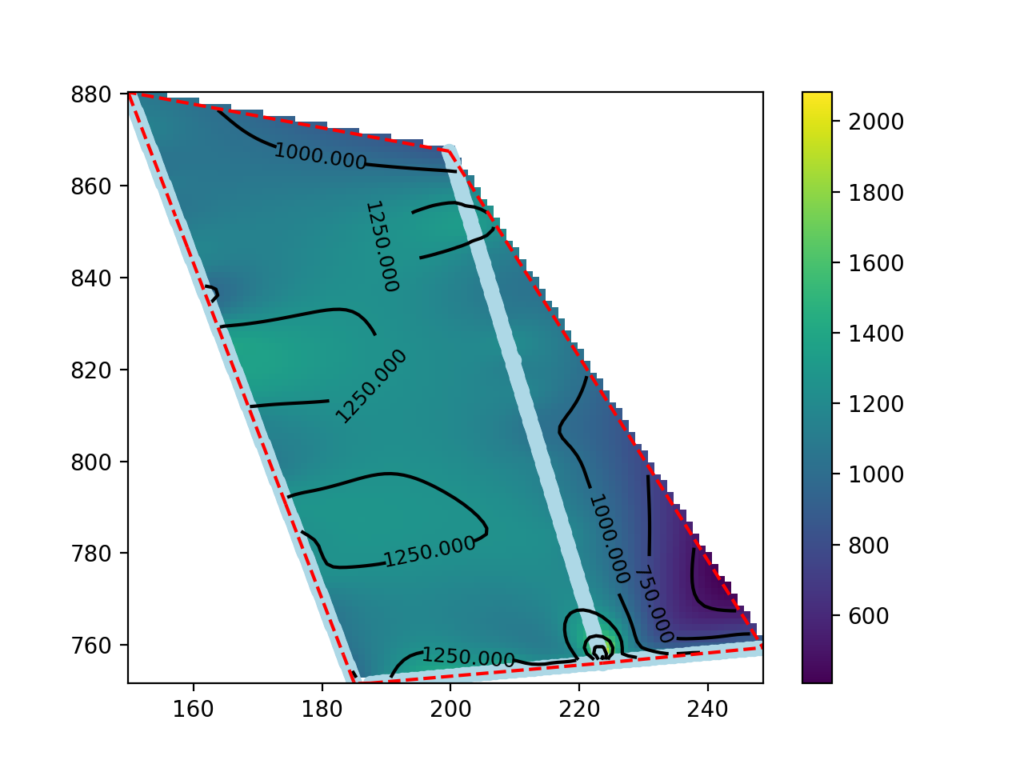
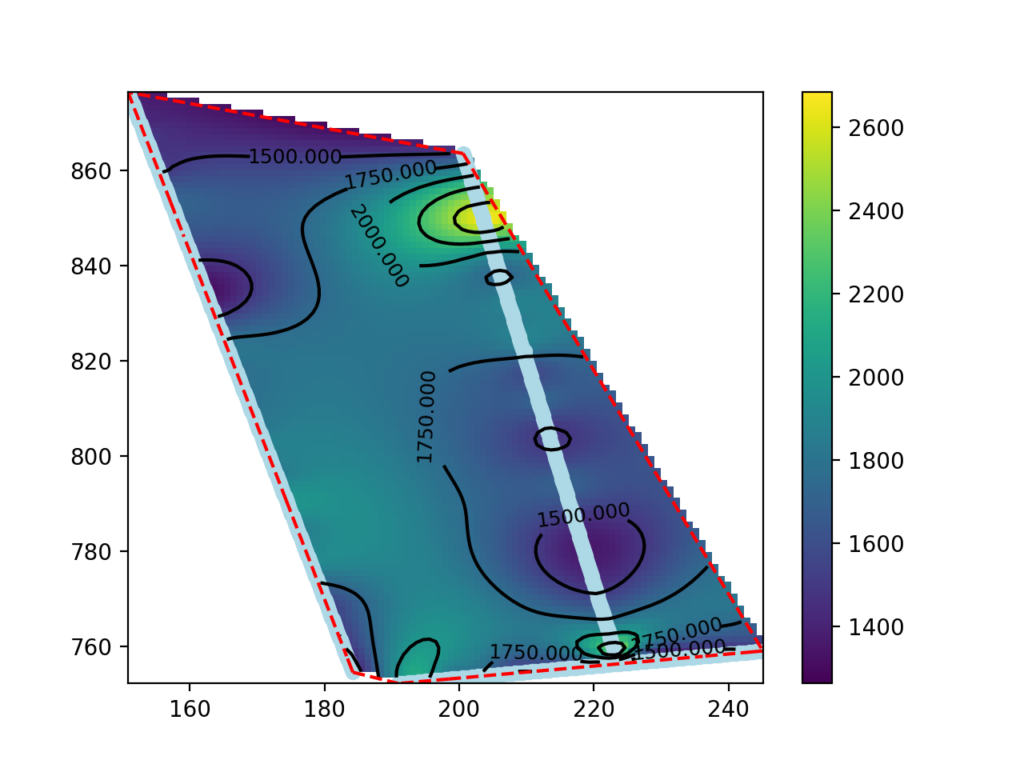
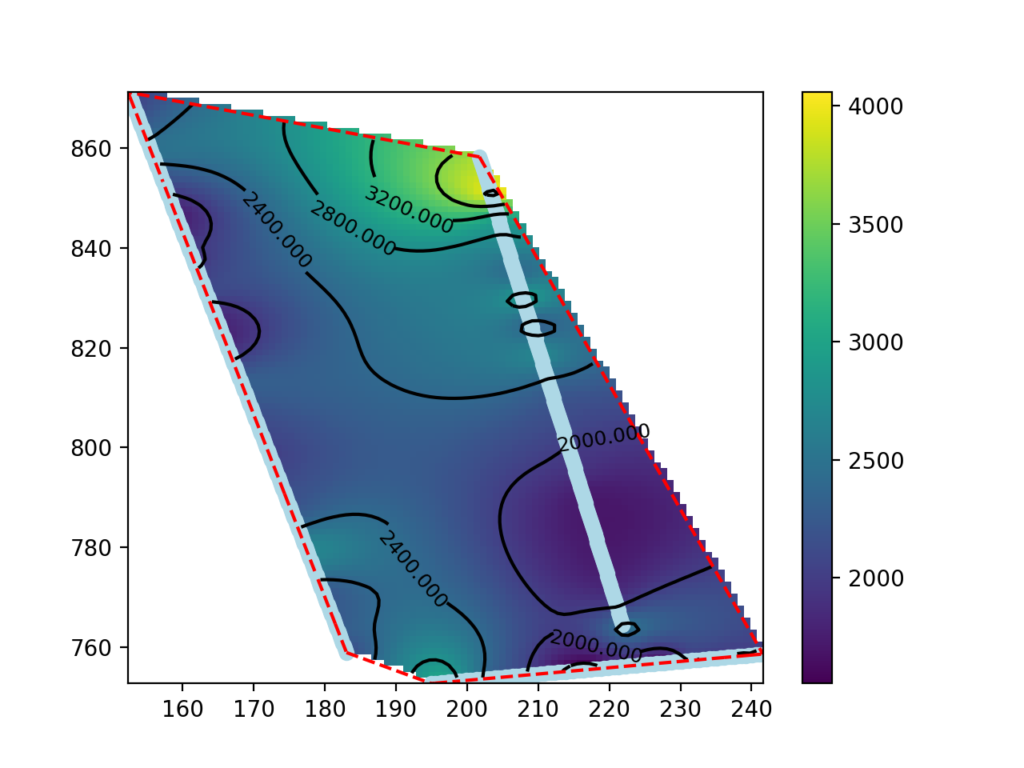
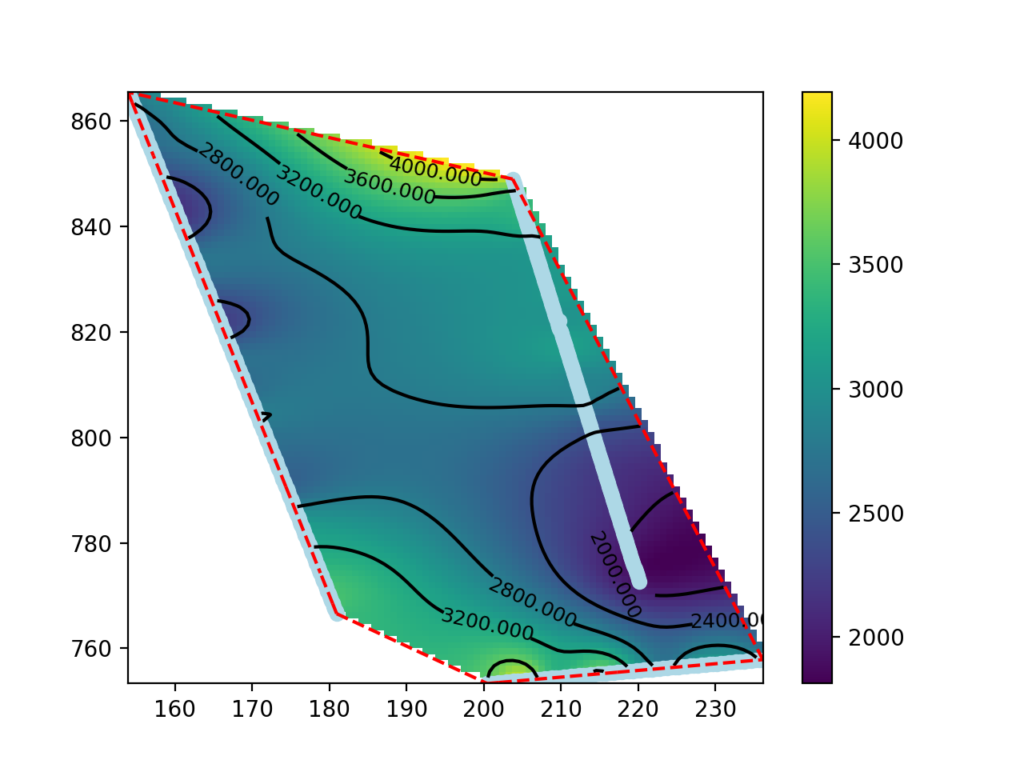
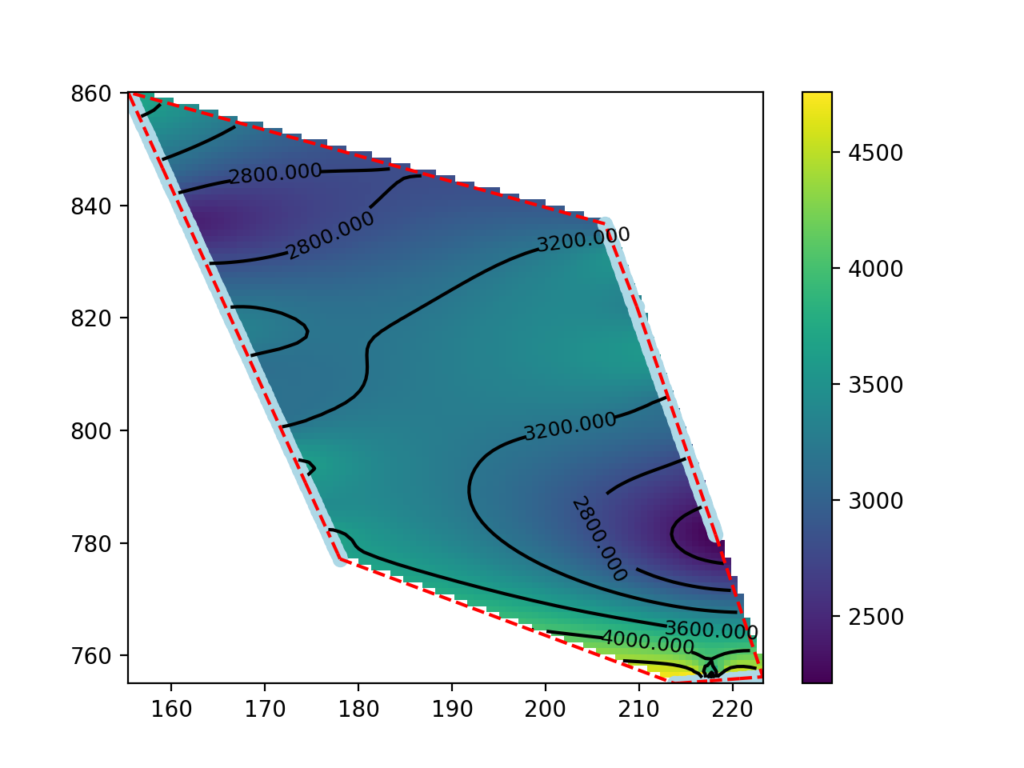
Questa guida presenta una procedura per realizzare delle mappe di velocità sismica a profondità definita usando i dati di tomografia sismica prodotti da SmartTomo adoperando strumenti free ed open source esterni a smartTomo.

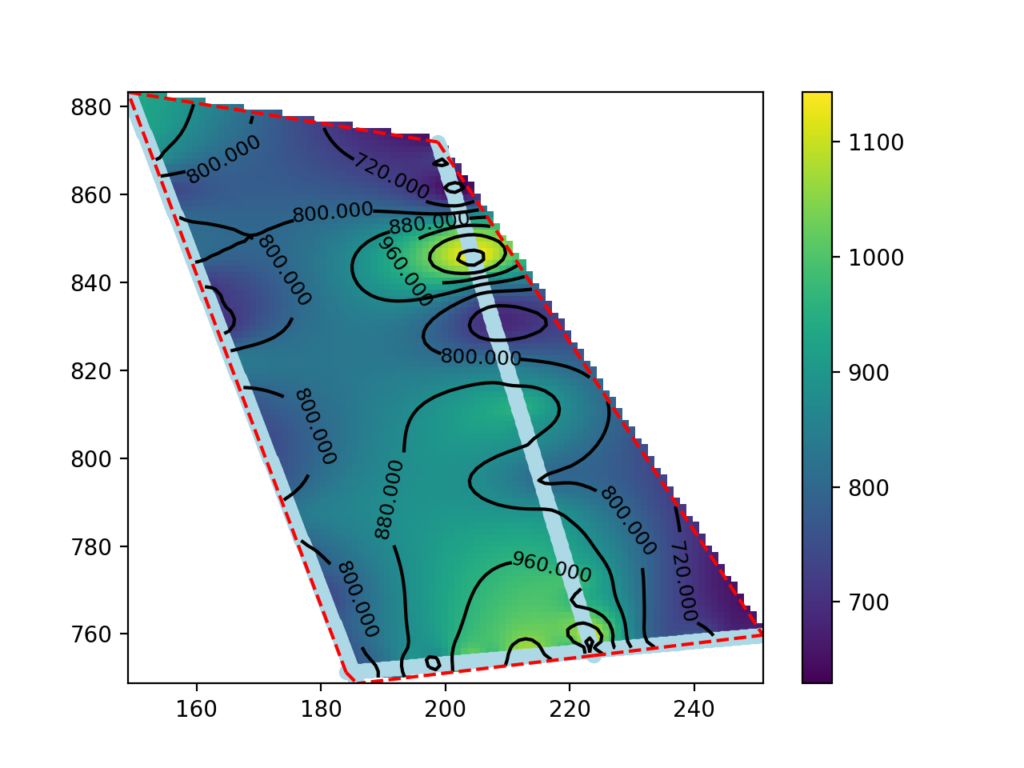
Per questo tutorial sono stati usati tre profili sismici georiferiti esportati come griglia di testo (per motivi di tutela della privacy le coordiante sono state trasformate). Le elaborazioni prevedono l’utilizzo di Python con i moduli Pandas, Numpy, Scipy e Matplotlib.

Scarica il codice completo dell’esempio e i dati da qui.

Dopo aver installato Python, i moduli possono essere installati con il comando pip eseguito dalla linea di comando (PowerShell su Windows):

python -m pip install numpy pandas scipy matplotlib

I dati della tomografia sismica esportati da SmartTomo sono formattati in una tabella separata da spazi salvata in un file di testo:

186.593449 745.829673 -0.250000 589.178237
186.461571 746.311968 -0.250000 596.123248
186.329694 746.794263 -0.250000 602.781370
186.197816 747.276558 -0.250000 608.095063
186.065939 747.758853 -0.250000 606.724411

Le coordinate (prima e seconsa colonna) e la profondità (terza colonna) corrispondono alla posizione e alla quota del centro della cella. La quarta colonna corrisponde alla velocità delle onde sismche in m/s.

I tre profili sismici sono salvati nei file L1.txt, L2.txt, L5.txt.

Vengono importati i moduli usati per questo esempio:

import pandas as pd          #import of modules
import numpy as np
from scipy.interpolate import RBFInterpolator # radial basis functions
from scipy.spatial import ConvexHull
import matplotlib.pyplot as plt

Vengono letti i dati (read_csv) dei tre profili dentro ad un DataFrame di Pandas e assegnato il nome alle colonne:

#loading of seismic profile exported as grid in to Pandas dataframe
l1 = pd.read_csv("L1.txt", sep=' ')      
l1.columns = ["X", "Y","Z","Speed"]

l2 = pd.read_csv("L2.txt", sep=' ')
l2.columns = ["X", "Y","Z","Speed"]

l5 = pd.read_csv("L5.txt", sep=' ')
l5.columns = ["X", "Y","Z","Speed"]

I dati delle tre linee vengono concatenati e vengono selezionati i dati alla profondità, ad esempio, di -5.25 metri. I dati selezionati vengono suddivisi in vettori contenenti solamente una variabile.

# Concatenate together all the seismic data
all_lines = pd.concat([l1,l2,l5])

# and select data at -5.25m depth
df = all_lines.loc[result["Z"] == -5.25]

# Extract and convert each column to Numpy arrays
X = df["X"].to_numpy()
Y = df["Y"].to_numpy()
Z = df["Z"].to_numpy()
V = df["Speed"].to_numpy()

Le coordinate contenute nei vettori X e Y vengono fuse insieme in una matrice chiamata coords e viene inizializzato l’interpolatore (RBFInterpolator) che sarà usato per costruire la mappa di velocità:

#paste together coordinates columns
coords = np.stack([X.ravel(),Y.ravel()],-1)

#inizialize interpolator based on RBF
rbf_int = RBFInterpolator(coords,V.ravel())

Viene realizzata la griglia rettangolare che contiene i dati delle tomografie sismiche con 100 celle per lato.

x_fine = np.linspace(X.min(), X.max(), 100)
y_fine = np.linspace(Y.min(), Y.max(), 100)
x_grid, y_grid = np.meshgrid(x_fine, y_fine)

grid = np.stack([x_grid.ravel(),y_grid.ravel()],-1)

Con la chiamata alla funzione rbf_int viene interpolata la velocità sulla griglia definita nel pasaggio precedente:

z_grid = rbf_int(grid).reshape(x_grid.shape)

Il blocco di codice seguente è dedicato alla visualizzazione della mappa. Viene prima creato l’oggetto grafico su cui viene disegnata la mappa di velocità (pcolormesh), i punti della tomografia sismica (scatter), il perimetro dell’area di interesse (plot), le isolinee (contour, clabel) e la scala di colore (colorbar)

fig, ax = plt.subplots()    #init enviroments
cm = ax.pcolormesh(x_fine, y_fine, z_grid) #draw the map and save the colormodel cm
p = ax.scatter(X,Y,color = "lightblue") #add the points corrisponding to  input data

# compute and draw the smallest convex set that contains input data
hull = ConvexHull(coords)
for simplex in hull.simplices:
    plt.plot(coords[simplex, 0], coords[simplex, 1], 'k--',color = "red")

# draw contour lines
CS = ax.contour(x_fine, y_fine, z_grid, 10, colors='k')  
ax.clabel(CS, fontsize=9, inline=True)

#add the color bar to the plot
fig.colorbar(cm)
#show the plot window
plt.show()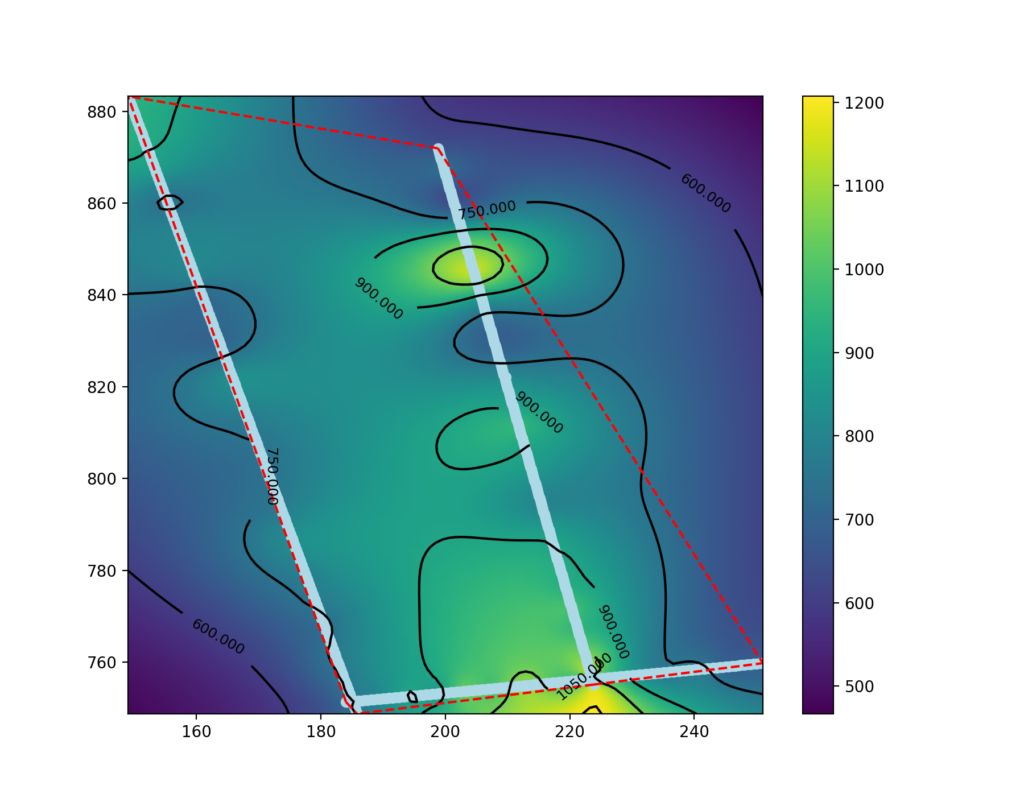

Scarica il codice completo dell’esempio e i dati da qui.

Visualizzare solamente la parte significativa della mappa.

La mappa che abbiamo realizzato nel paragrafo precedente mostra i dati anche all’esterno delle area compresa tra le linee sismiche. I dati in queste aree sono estrapolati e pertanto possono essere non significativi.

Qui di seguito vedremo come eliminare i punti esterni e visualizzare solo i valori compresi nel perimetro che inscrive i dati di input. All’inizio del codice del paragrafo precedente inserite la seguente funzione per calcolare quali punti cadono all’interno del convex hull:

# code from https://stackoverflow.com/a/16898636
def in_hull(p, hull):
    """
    Test if points in `p` are in `hull`

    `p` should be a `NxK` coordinates of `N` points in `K` dimensions
    `hull` is either a scipy.spatial.Delaunay object or the `MxK` array of the 
    coordinates of `M` points in `K`dimensions for which Delaunay triangulation
    will be computed
    """
    from scipy.spatial import Delaunay
    if not isinstance(hull,Delaunay):
        hull = Delaunay(hull)

    return hull.find_simplex(p)>=0

Prima del blocco di codice dedicato alla rappresentazione dei risultati, i dati della griglia possono essere filtrati per eliminare i dati esterni al perimetro:

inhull = in_hull(grid,coords)
i=0
j=0
k=0
for z in z_grid:
    j = 0
    for zz in z:
        if inhull[i] == False:
            z_grid[k][j] = np.nan
        i= i + 1
        j= j + 1
    k = k + 1

In questo modo i punti esterni vengono impostati ad un valore corrisponente a np.nan (not a number) che viene ignorato nella fase di disegno del grafico.